Numerical Methods for Matter in GR

Ian Hawke

github.com/IanHawke
orcid.org/0000-0003-4805-0309
STAG, University of Southampton

ianhawke.github.io/slides/et-2023

What matters

$$ G_{ab} = 8 \pi T_{ab}, \quad \textrm{where } T_{ab} = \dots $$

scalar fields;
simple fluids (dust, barotropes);
finite $T$, real $Y_\text{x}$ fluids;
electromagnetism (MHD, resistivity, ...);
neutrinos, ...

ETK:

couple $T_{ab} \leftrightarrow G_{ab}$;
provides solvers for perfect MHD, constituitive interfaces;
builds on spacetime infrastructure.

Hammond+, 2205.11377.

Conservation

EFEs imply $\nabla_a T^{ab} = 0$.

Pick a tetrad, $e_b^{(j)}$ to get $$ \begin{aligned} && \nabla_a \left[ e_b^{(j)} T^{ab} \right] &= \tfrac{1}{\sqrt{-g}} \partial_a \left( \sqrt{-g} e_b^{(j)} T^{ab} \right) = -T^{ab} \nabla_a e_b^{(j)} \\ \implies && \partial_t {\bf q} + \partial_i {\bf f}^{(i)}({\bf q}) &= {\bf s}. \end{aligned} $$ Balance law form.

Only four equations: need other constituitive equations for, eg, EM, particle number, etc.

Relations may need variables other than ${\bf q}$: conservative to primitive problem.

We now know the outlines of our problem. We want a model of matter, coupled to GR, that we can write as a set of PDEs. This model will encode the detailed physics we're interested in, at the level we can simulate with our given resources. But before we try and be specific, let's look at what we can say in general.
We know the field equations require total stress energy conservation: the divergence of $T^{ab}$ is zero. We can use this to get four equations of motion. The most useful form for our purposes is to use the standard identity for the 4-divergence of a vector, which can be written as the partial 4-divergence of that vector, weighted by the metric determinant. To get from the stress-energy, which is a two-tensor, to a vector, we contract the free index with one member of a tetrad, which is a set of orthonormal (in our case) vectors that we can link to the coordinates. This then allows us to write stress energy conservation as four PDEs, one for each member of the tetrad.
The key point is that the only derivatives of the matter appear in total divergence form. The term on the right-hand-side which isn't in this form only involves derivatives of the tetrad, which can be written as derivatives of spacetime quantities. We write this abstractly in balance law form: all derivatives of the matter are total derivatives, but these fluxes must balance off against the source terms which come from the geometry.
If we simplify to Minkowski space in standard Cartesian coordinates then the source terms vanish and these balance laws reduce to the conservation laws for energy-momentum. However, we need to be careful of this interpretation (locally): if we write Minkowski spacetime in spherical coordinates then there will be source terms, but that certainly does not mean that energy-momentum is being transferred between the matter and the spacetime.
The final point is that the four conserved quantities q will not necessarilly be useful for the constituitive or closure relations that we need. In particular, the fluxes are often only easily written in terms of other variables. The key example is the equation of state, which is usually written in terms of thermodynamic potentials such as density and temperature which are not transparent from the conserved quantities. This is the conservative to primitive problem which in general is expensive and complex: rely on existing solutions (eg Reprimand).

Shock formation

Advection equation $$ \partial_t q + \partial_x (v q) = 0. $$ Information moves right, speed $v$.

Burgers equation $$ \partial_t q + \tfrac{1}{2} \partial_x q^{2} = 0. $$ Information moves right, speed $q$.

Shocks form.

We see that generically the matter will obey conservation laws. We expect the fluxes ${\bf f}$ to depend nonlinearly on the conserved variables ${\bf q}$. This immediately tells us something very important.
The simplest conservation law is the advection equation, where the solution is propagated to the right with constant speed $v$. For a nonlinear conservation law we can locally approximate it as an advection-like equation, where the solution propagates with speed $\partial_q f$. This means the propagation speed depends on the data. Depending on the form of the flux function, some gradients will steadily get steeper, and some will get shallower. In the absence of dissipation (and crucially the generic total energy-momentum equations have no dissipative terms) these steepening effects will lead to discontinuities: a generic shock will form.

Nonlinearity

Formally need to work with weak form

$$ \begin{aligned} && \partial_t q + \nabla_k f^{(k)}(q) & = 0 \\ \implies && \frac{\text{d}}{\text{d}t} \int_V q + \oint_{\partial V} \hat{n}_k f^{(k)}(q) & = 0. \end{aligned} $$

Discrete version, 1d:

$$ \frac{\text{d}}{\text{d}t} \hat{q}_i + \frac{1}{\Delta x} \left[ f_{i+1/2} - f_{i-1/2} \right] = 0. $$

Finding the flux $f_{k \pm 1/2}$ depends on the model (for fluids see GRHydro etc).

Consistency

Using the right weak form is essential.

$$ \begin{aligned} && \partial_t q^n + \frac{n}{n+1} \partial_x q^{n+1} & = 0 \\ \implies && \partial_t q + q \partial_x q & = 0. \end{aligned} $$

Strong solutions agree when continuous; inconsistent at shocks.

Can use entropy pairs, path-consistent methods for complex cases.

Getting shock propagation speeds right is essential and depends both on how the model is written and how the numerical method implements it. A standard example is shown on the slide, where - if we were only dealing with differentiable solutions - the results should be identical for all values of n. However, as soon as a discontinuity forms, its speed depends strongly on the value of n. This means that manipulating a balance law for numerical advantage has to be done with care, as both the model and the numerics need to be consistent.
The point here is that there can be multiple, even infinite, weak solutions that could in principle evolve from discontinuous data. With standard methods the choice of weak form implicitly picks out which weak solution is chosen by the numerics. We'll come back to this.
Finally, there is the concern of what to do when you don't have a natural balance law form, or can't write your equations as a total derivative at all. Superfluids and other multi-fluid problems have this issue. In this case you have to explicitly state what the dissipation operator is and construct a scheme to use that entropy.

Algorithm outline

Discrete version, 1d:

$$ \frac{\text{d}}{\text{d}t} \hat{q}_i + \frac{1}{\Delta x} \left[ f_{i+1/2} - f_{i-1/2} \right] = 0. $$

Reconstruct $\{ \hat{q}_i \} \to q(x)$;
Solve discontinuous problem at cell boundaries.

Sources "just" add (stiffness?);
Can reconstruct $f$ directly;
Use MoL in time;
High accuracy needs good reconstruction and time evolution.

The classic algorithm used by Einstein Toolkit codes works as follows.
The weak solution is stored as an integral average over the grid cells. Using the weak form we write the update in terms of the flux through the boundary of the cell. In one dimension that's the flux contributions into the cell from the left and out through the right.
We then take these integral average solutions and reconstruct a pointwise function interpolating the data. This has to ensure conservation of the data, or shocks are inconsistent. It has to allow for discontinuities: all practical methods put discontinuities at the cell boundaries. So generically we assume that the data is always discontinuous at cell boundaries.
We then need to solve this discontinuous problem at the boundary to compute the flux. This is usually called the Riemann Problem. Strictly the Riemann Problem finds the solution for all variables, and we then construct the flux from them (using self-similarity). However, we can (and often do) use approximations that give the flux directly from the variables.
We can then update the discrete integral averages using the flux contributions. This is often talked about as updating the reconstructed solution which is then integral averaged back onto the discrete cells.
Adding sources can be done algebraically. Provided they change slowly in time, which is true for the geometric terms, this is fine. To evolve in time we use the standard method of lines approach. Both absolute and order of accuracy are dominated by the reconstruction method, with some impact from the time evolution. The Riemann solver has an impact near shocks and ensures stability.

Reconstruction

Any high order method shows Gibbs' oscillations at jumps.

No convergence with resolution.

Use piecewise polynomial reconstruction (eg WENO) to avoid oscillations.

Converges with resolution.
Formally first order at jumps.
Much more expensive than linear FD.
Extension to higher dimensions an issue.
Total variation $\sup_i \sum | {\bf q}_{i+1} - {\bf q}_i |$ bounded.

See GRHydro, IllinoisGRMHD, Spritz, WhiskyTHC.

If reconstruction dominates the accuracy of the scheme, we want to make it as accurate as possible. We'd usually do this using as much discrete data as possible with a smooth polynomial. Unfortunately that fails.
The standard Gibbs' effect is usually introduced in terms of Fourier series but can be seen in other function basis representations. That is, when a finite amount of data is used to represent a discontinuous jump in a field, the truncated series approximation will oscillate near that jump. When we differentiate the approximation in order to approximate the derivative of the original field, those oscillations are amplified. As Gibbs' oscillations do not converge with amplitude as the order of the truncation is increased, this means the oscillations in the approximate derivative get worse as more computational effort is used.
For finite difference methods these oscillations exist but are confined to a region near the jumps. As spectral methods rely on a dense differentiation matrix, the oscillations induced contaminate the entire domain.
The alternative that avoids, or at least minimises, the oscillations, is to change the data used in the interpolating polynomial to avoid the jump. This ensures that Gibbs' oscillations are never introduced, so the derivative is fine. However, it means that the reconstruction step now depends on the data itself. There are many ways of doing this, from second order slope limited methods to high order WENO methods. Whilst they are essential for discontinuous data they are much more costly - in some cases an order of magnitude or more - than finite differencing.
These sort of reconstruction methods can be found in a number of thorns in the ETK. If developing your own code then for initial tests I would recommend taking the slope limited methods from, for example, GRHydro, but higher order methods will be essential eventually. For those I would recommend starting with the WENO methods which are most generically implemented in WhiskyTHC.
As a theory matter, the crucial point here is that we need to constrain the total variation of the solution. Intuitively, this is linked to the maximum size of any jump in the discrete data. If this is unbounded the solutions won't converge, so this is a crucial restriction.

Riemann Solvers

Reconstruction $\to$ Riemann Problem;
Full solution as waves: expensive;
Approximations usually enough;

Roe - linearize:

sharp;
entropy violations.

Marquina - fixes Roe:

flux formula only;
expensive.

HLL(E) - impose number of waves:

cheap;
positive;
diffusive.

Given the reconstructed data we now need to solve for the flux at cell boundaries. We can approximate the problem at cell boundaries as being piecewise constant - this is accurate enough. This is known as the Riemann Problem, where we need to know how the solution evolves in time.
In this sketch picture we see the density evolving with time, splitting into three waves: rarefaction, contact, and shock. We rely on the self-similarity of the problem: from the solution along the axis we have the solution for all future time, from which we compute the flux.
Unfortunately, finding the full solution with all waves correct is far too expensive - try using Bruno's solver for MHD to see the cost. Also it's not needed in evolution codes, as approximations are enough.
Most approximations to the solution look at the waves in parameter space - here the x axis is still space but the vertical axis is time. The wave structure shows the self-similarity: each line is straight, and the solution between waves is constant. The real cost in finding the exact solution is iteratively finding the correct wave structure, so most approximations start with that wave structure. Here I note three approaches, all seen in GRHydro.
For Roe's solver we linearize the nonlinear flux (in particular, its Jacobian) about some state. That makes the problem linear and hence easy to compute. It gives very sharp discontinuous waves but isn't good at continuous waves and can fail horribly when a transsonic rarefaction appears.
Marquina fixes Roe by checking for transsonic rarefactions and replacing the flux computed then. This is highly accurate, but is expensive and only gives the flux directly, without going through the solution.
Finally, the least accurate but most robust solution comes from the HLL family of solvers. In this case the wave speeds are over-estimated and only a limited number of waves are used. We can then enforce conservation to get the solution. This is the standard solver to start with - it can smear out shocks, but with good reconstruction methods is often enough. HLL also guarantees that certain quantities that you want to remain positive (like density) do so.

Entropy functions

Entropy $\eta({\bf q})$ is convex function, flux $\psi$, s.t.

$$ \partial_t \eta + \partial_x \psi \le 0, \quad \nabla_{\bf q} \psi = \nabla_{\bf q} \eta \nabla_{\bf q} {\bf f}. $$

Entropy picks out unique weak solution.

Given two solutions ${\bf q}_{1, 2}$, then

$$ \frac{d}{dt} \| {\bf q}_{1} - {\bf q}_{2} \| \le 0 $$

only if both are entropy solutions.

Conclusion: if numerical scheme violates entropy condition, it can and will diverge from true solution.

Finally, an underlying point is entropy. I've noted that Roe has problems for transsonic cases. I've noted that multiple weak solutions can be consistent with given initial data. So the question is how we enforce that we get the right solution.
The sketch on the right illustrates the problem. We have a Riemann problem with separating data, as seen from the characteristic speeds. We expect to get the rarefaction solution at the top. This is because if we perturbed the initial data very slightly, smoothing it out, then the characteristic speeds should vary in exactly this way. However, both of the weak solutions below are consistent with the discontinuous data. They do something very odd - information appears out of the shock discontinuously - but mathematically they are fine.
To fix this problem we have to find an entropy pair: a scalar function of the conserved quantities that is convex, called the entropy, and its associated flux. This pair satisfies a conservation law, where the entropy strictly decreases only at shocks. Yes, decreases: blame numerical analysts for this choice.
Entropy solutions satisfy the conservation laws and the entropy law. If our numerical solution also obeys the entropy law then it will converge to some solution of the real problem. In essence, entropy solutions enforce that characteristics also propagate into shocks, not out of them.
Now, Murphy's law says that if we don't enforce that our numerical scheme obeys the entropy condition then it violates it. The corollary to the above is that an entropy violating solution will not converge to any solution of the original problem. So entropy consistency is essential.
It turns out that a consitent entropy stable flux (so, not Roe), combined with the telescoping flux form, enforces an entropy solution. Combine that with total variation boundedness and we can be confident that we're getting the right thing. However, the approaches can be overly restrictive.

MHD

Still conservation laws (ideal case).
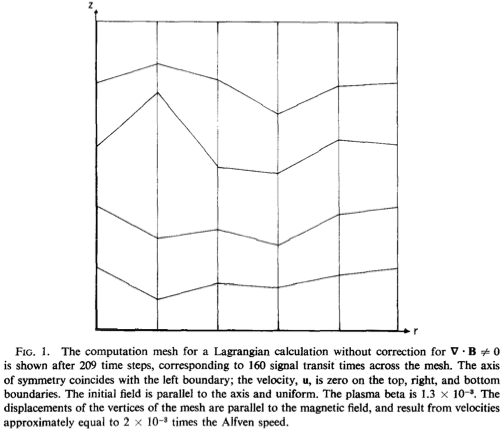
Constraint $\mathcal{C} = \nabla \cdot {\bf B} \equiv 0$ essential.
Can either

add damping terms $\propto - \mathcal{C}$
enforce $\mathcal{C}=0$ discretely.

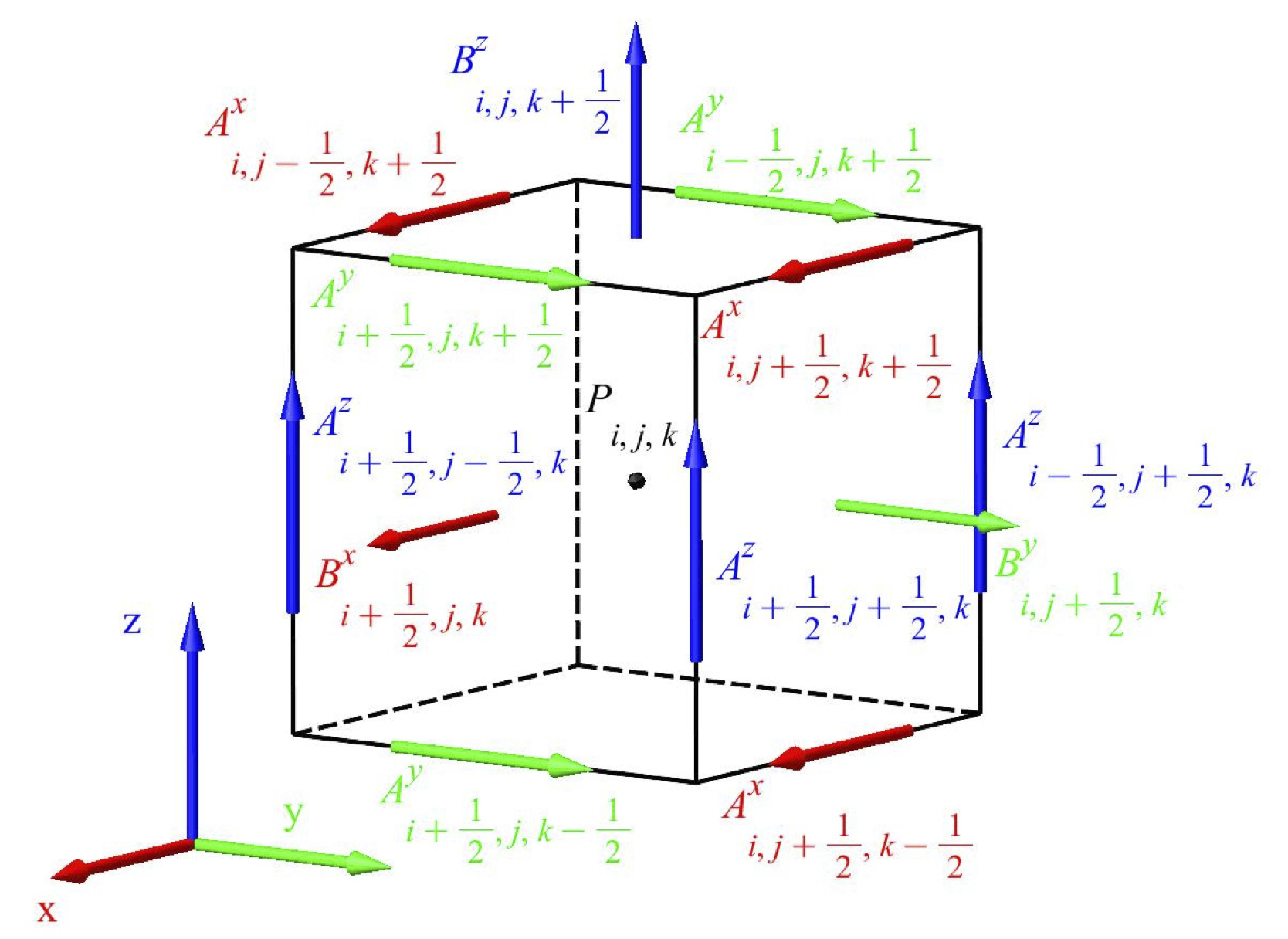
Using vector potential does the latter - preferred.
Entropy function evolution has term $\propto \mathcal{C}$

Brackbill and Barnes

Cipolletta+

Finally, we need to discuss the additional issues that come in when we add physics beyond just perfect fluids. We'll focus on MHD. In this case the Maxwell equations are easily written as balance laws, but there is the no monopole divergence constraint as well.
It's been known for a very long time that ensuring the divergence constraint holds is crucial - the figure here is from Brackbill and Barnes from 1980. Since then a number of approaches have been tried. In constraint damping terms are added proportional to the constraint (which should vanish) so that the evolution of the error converges to zero exponentially. Every time numerical error kicks the divergence away from zero, the damping term forces it back.
The alternative approach is to enforce the constraint at the discrete level. This should be compared to the way that a telescoping flux enforces conservation at the discrete level. One method, used by IllinoisGRMHD and Spritz, is to evolve a vector potential stored at cell edges. The magnetic field is then the curl of the vector potential, which is divergence free by construction.
It's worth noting that entropy pairs have been constructed for MHD (in general, and for relativistic MHD for simple equations of state). With this entropy pair we see that the evolution of the entropy has a term that is proportional to the divergence constraint. The proportionality constant is nonlinear and complex. Again, Murphy's law says that unless we explicitly enforce otherwise, a violation of the divergence constraint will make the entropy grow with the wrong sign, and lead to convergence to the wrong solution.

Summary

ETK matter simulations

focus on finite volume approaches;
are "good enough" (?) for LIGO, but...
are costly, inaccurate (compared to spacetime).

Focus on shocks important, but restricts accuracy.

Long term accuracy needs better approaches (DG, compact FD will help).

Fast/short effects need LES-type treatment.

Entropy stability only non-negotiable.

Hammond+; Most+.

The steps I've outline above form the basis of the astrophysical ETK evolution codes involving matter. They've been good enough for now, but the costs are high and the accuracy low compared to spacetime codes. For next generation detectors we need order of magnitude improvements.
A lot of the focus in the field has been ensuring correct evolution at shocks. This is essential, but shocks form a tiny region of the spacetime. By indirectly enforcing entropy stability and TVB at every point in spacetime we are restricting accuracy. Methods that focus on different metrics for accuracy such as compact differencing schemes could give significant improvements.
Finally, we should note that matter evolution, particularly through merger, can see lots of structure and power built up on short lengthscales and fast timescales, below the scales that we can resolve on the grid. There's a lot of effort right now to capture this physics using LES-type approaches, which are naturally ad hoc. However, ensuring stability with these ad hoc terms need analysis that hasn't yet been done: I believe entropy stability should be the non-negotiable basis on which we build future schemes.
Thank you for your attention.